Exploratory Data Analysis-A first look at the data.

 

Exploratory Data Analysis

A first look at the data.

 

	Type-1
Type-2	Graphical	Non-Graphical	ROLE	TYPE
Univariate	Univariate Graphical	Univariate Non-Graphical	Outcome role & Explanatory role	Categorical Type and Quantitative Type
Multivariate	Multivariate Graphical	Multivariate Non-Graphical
	Summarize the data in a diagrammatic or pictorial way.	Calculation of summary statistics

 

Univariate Non-Graphical	Categorical data
The characteristics of interest	The characteristics of interest for a categorical variable are simply the range of values and the frequency (or relative frequency) of occurrence for each value.
Univariate non-graphical techniques	Therefore, the only useful univariate non-graphical techniques for categorical variables is some form of tabulation of the frequencies, usually along with calculation of the fraction (or percent) of data that falls in each category.
Example	For example, if we categorize grades as Matric, Fsc, Bsc and “other”, then there is a true population of all students enrolled in the 2007 Fall semester. If we take a random sample of 20 students EDA would look like this:
	Statistic/College Matric Fsc Bsc other Total Count 5 6 4 5 20 Proportion 0.25 0.30 0.20 0.25 1.00 Percent 25% 30% 20% 25% 100%

 

Univariate Non-Graphical	Quantitative data
The characteristics of interest	The characteristics of the population distribution of a quantitative variable are its center, spread, modality (number of peaks in the pdf), shape (including “heaviness of the tails”), and outliers.
	Univariate EDA for a quantitative variable is a way to make preliminary assessments about the population distribution of the variable using the data of the observed sample.
	For quantitative variables (and possibly for ordinal variables) it is worthwhile looking at the central tendency, spread, skewness, and kurtosis of the data for a particular variable from an experiment. But for categorical variables, none of these make any sense.
Univariate non-graphical techniques	If the quantitative variable does not have too many distinct values, a tabulation, as we used for categorical data, will be a worthwhile univariate, non-graphical technique.
	But mostly, for quantitative variables we are concerned here with the quantitative numeric (non-graphical) measures which are the various sample statistics.  In fact, sample statistics are generally thought of as estimates of the corresponding population parameters.
	We can calculate “sample statistics” from the data, such as sample mean, sample variance, sample standard deviation, sample skewness and sample kurtosis.
Sample Distribution	The sample of measurements of a particular variable, , we select for our particular experiment for observation is called “sample distribution”.
Central Tendency	The central tendency or “location” of a distribution has to do with typical or middle values. The common, useful measures of central tendency are the statis tics called (arithmetic) mean, median, and sometimes mode.
Arithmetic Mean	The arithmetic mean is simply the sum of all of the data values divided by the number of values. It can be thought of as how much each subject gets in a “fair” re-division of whatever the data are measuring.
	For any symmetrically shaped distribution (i.e., one with a symmetric histogram or pdf or pmf) the mean is the point around which the symmetry holds.
	For non-symmetric distributions, the mean is the “balance point”
Median	The median is another measure of central tendency. The sample median is the middle value after all of the values are put in an ordered list. If there are an even number of values, take the average of the two middle values.
	For symmetric distributions, the mean and the median coincide. For unimodal skewed (asymmetric) distributions, the mean is farther in the direction of the “pulled out tail” of the distribution than the median is. Therefore, for many cases of skewed distributions, the median is preferred as a measure of central tendency.
	The median has a very special property called robustness. A sample statistic is “robust” if moving some data tends not to change the value of the statistic. The median is highly robust, because you can move nearly all of the upper half and/or lower half of the data values any distance away from the median without changing the median. More practically, a few very high values or very low values usually have no effect on the median.
Mode	A rarely used measure of central tendency is the mode, which is the most likely or frequently occurring value.
	More commonly we simply use the term “mode” when describing whether a distribution has a single peak (unimodal) or two or more peaks (bimodal or multi-modal).
	In symmetric, unimodal distributions, the mode equals both the mean and the median.
	In unimodal, skewed distributions the mode is on the other side of the median from the mean.
	In multi-modal distributions there is either no unique highest mode, or the highest mode may well be unrepresentative of the central tendency.
Spread	Spread is an indicator of how far away from the center we are still likely to find data values.
variance	The variance is a standard measure of spread.
	The variance and standard deviation are two useful measures of spread. The variance is the mean of the squares of the individual deviations. The standard deviation is the square root of the variance. For Normally distributed data, approximately 95% of the values lie within 2 sd of the mean.
Standard Deviation	The standard deviation is simply the square root of the variance. Therefore it has the same units as the original data, which helps make it more interpretable.
interquartile range	−   A third measure of spread is the interquartile range. To define IQR, we first need to define the concepts of quartiles.
	The quartiles of a population or a sample are the three values which divide the distribution or observed data into even fourths.
	So one quarter of the data fall below the first quartile, usually written Q1; one half fall below the second quartile (Q2); and three fourths fall below the third quartile (Q3).
	The astute reader will realize that half of the values fall above Q2, one quarter fall above Q3, and also that Q2 is a synonym for the median.
	Once the quartiles are defined, it is easy to define the IQR as IQR = Q3  Q1. By definition, half of the values (and specifically the middle half) fall within an interval whose width equals the IQR. If the data are more spread out, then the IQR tends to increase, and vice versa.
	The IQR is a more robust measure of spread than the variance or standard deviation. Any number of values in the top or bottom quarters of the data can be moved any distance from the median without affecting the IQR at all. More practically, a few extreme outliers have little or no effect on the IQR.
Range	The range of a sample is the distance from the minimum value to the maximum value: range = maximum - minimum.
	In contrast to the IQR, the range of the data is not very robust at all.  If you collect repeated samples from a population, the minimum, maximum and range tend to change drastically from sample to sample, while the variance and standard deviation change less, and the IQR least of all.
	The minimum and maximum of a sample may be useful for detecting outliers, especially if you know something about the possible reasonable values for your variable. They often (but certainly not always) can detect data entry errors such as typing a digit twice or transposing digits (e.g., entering 211 instead of 21 and entering 19 instead of 91 for data that represents ages of senior citizens.)
	The IQR has one more property worth knowing: for normally distributed data only, the IQR approximately equals 4/3 times the standard deviation. This means that for Gaussian distributions, you can approximate the sd from the IQR by calculating 3/4 of the IQR.
Skewness	Two additional useful univariate descriptors are the skewness and kurtosis of a distribution. Skewness is a measure of asymmetry.
Kurtosis	Kurtosis is a measure of “peakedness” relative to a Gaussian shape.
	Skewness is a measure of asymmetry. Kurtosis is a more subtle mea sure of peakedness compared to a Gaussian distribution.

 

 

Univariate graphical EDA	Categorical Data
	While the non-graphical methods are quantitative and objective, they do not give a full picture of the data; therefore, graphical methods, which are more qualitative and involve a degree of subjective analysis, are also required.
Histograms	The only one of these techniques that makes sense for categorical data is the histogram (basically just a barplot of the tabulation of the data).
	A pie chart is equivalent, but not often used. The concepts of central tendency, spread and skew have no meaning for nominal categorical data. For ordinal categorical data, it sometimes makes sense to treat the data as quantitative for EDA purposes; you need to use your judgment here
	The most basic graph is the histogram, which is a barplot in which each bar represents the frequency (count) or proportion (count/total count) of cases for a range of values. Typically the bars run vertically with the count (or proportion) axis running vertically. To manually construct a histogram, define the range of data for each bar (called a bin), count how many cases fall in each bin, and draw the bars high enough to indicate the count.
	histograms are one of the best ways to quickly learn a lot about your data, including central tendency, spread, modality, shape and outliers.
A stem and leaf plot	A stem and leaf plot shows all data values and the shape of the distribution.
Boxplots	Boxplots are very good at presenting information about the central tendency, symmetry and skew, as well as outliers, although they can be misleading about aspects such as multimodality. One of the best uses of boxplots is in the form of side-by-side boxplots (see multivariate graphical analysis below).
		The boxplot consists of a rectangular box bounded above and below by “hinges” that represent the quartiles Q3 and Q1 respectively, and with a horizontal “median” line through it. You can also see the upper and lower “whiskers”, and a point marking an “outlier”. The vertical axis is in the units of the quantitative variable.

 

Let’s assume that the subjects for this experiment are hens and the data represent the number of eggs that each hen laid during the experiment. We can read certain information directly off of the graph. The median (not mean!)  is 4 eggs, so no more than half of the hens laid more than 4 eggs and no more than half of the hens laid less than 4 eggs. (This is based on the technical definition of median; we would usually claim that half of the hens lay more or half less than 4, knowing that this may be only approximately correct.) We can also state that one quarter of the hens lay less than 3 eggs and one quarter lay more than 5 eggs (again, this may not be exactly correct, particularly for small samples or a small number of different possible values). This leaves half of the hens, called the “central half”, to lay between 3 and 5 eggs, so the interquartile range (IQR) is Q3-Q1=5-3=2.

 

Multivariate non-graphical EDA	Categorical Data
	Multivariate non-graphical EDA techniques generally show the relationship be tween two or more variables in the form of either cross-tabulation or statistics.
Cross-tabulation	For categorical data (and quantitative data with only a few different values) an extension of tabulation called cross-tabulation is very useful.
	For two variables, cross-tabulation is performed by making a two-way table with column headings that match the levels of one variable and row headings that match the levels of the other variable, then filling in the counts of all subjects that share a pair of levels. The two variables might be both explanatory, both outcome, or one of each. Depending on the goals, row percentages (which add to 100% for each row), column percentages (which add to 100% for each column) and/or cell percentages (which add to 100% over all cells) are also useful.
	Subject ID Age Group Sex GW young F JA middle F TJ young M JMA young M JMO middle F JQA old F AJ old F MVB young M WHH old F JT young F JKP middle M	Age Group / Sex Female Male Total young 2 3 5 middle 2 1 3 old 3 0 3 Total 7 4 11
	Table.1: Sample Data for Cross-tabulation	Table.2: Cross-tabulation of Sample Data
	Here is an example of a cross-tabulation. Consider the data in table.1. For each subject we observe sex and age as categorical variables.	We can easily see that the total number of young females is 2, and we can calculate, e.g., the corresponding cell percentage is 2/11 × 100 = 18.2%, the row percentage is 2/5 × 100 = 40.0%, and the column percentage is 2/7 × 100 = 28.6%.
	Cross-tabulation can be extended to three (and sometimes more) variables by making separate two-way tables for two variables at each level of a third variable.
Correlation	Another statistic that can be calculated for two categorical variables is their corre lation.
	The correlation between two random variables is a number that runs from -1 through 0 to +1 and indicates a strong inverse relationship, no relationship, and a strong direct relationship, respectively.
	For two quantitative variables, the basic statistics of interest are the sample co- variance and/or sample correlation, which correspond to and are estimates of the corresponding population parameters.
Covariance	The sample covariance is a measure of how much two variables “co-vary”, i.e., how much (and in what direction) should we expect one variable to change when the other changes.
	Positive covariance values suggest that when one measurement is above the    mean the other will probably also be above the mean, and vice versa. Negative covariances suggest that when one variable is above its mean, the other is below its mean. And covariances near zero suggest that the two variables vary independently of each other.
	Technically, independence implies  zero correlation, but the reverse is not necessarily true.
	Covariances tend to be hard to interpret, so we often use correlation instead. The correlation has the nice property that it is always between -1 and +1, with -1 being a “perfect” negative linear correlation, +1 being a perfect positive linear correlation and 0 indicating that X and Y are uncorrelated. The symbol r or rx,y is often used for sample correlations.

 

Multivariate graphical EDA
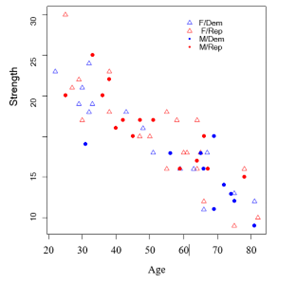
	There are few useful techniques for graphical EDA of two categorical random variables. The only one used commonly is a grouped barplot with each group rep- resenting one level of one of the variables and each bar within a group representing the levels of the other variable.

 

	Univariate graphs by category
	When we have one categorical (usually explanatory) and one quantitative (usually outcome) variable, graphical EDA usually takes the form of “conditioning” on  the categorical random variable.
	This simply indicates that we focus on all of  the subjects with a particular level of the categorical random variable, then make plots of the quantitative variable for those subjects.
Boxplots	We repeat this for each level of the categorical variable, then compare the plots. The most commonly used of these are side-by-side boxplots, as in figure. Side-by-side boxplots are the best graphical EDA technique for examining the relationship between a categorical variable and a quantitative variable, as well as the distribution of the quantitative variable at each level of the categorical variable.
	Here we see the data  which consists of strength data for each of three age groups. You can see the downward trend in the median as the ages increase. The spreads (IQRs) are similar for the three groups. And all three groups are roughly symmetrical with one high strength outlier in the youngest age group.
scatterplot	For two quantitative variables, the basic graphical EDA technique is the scatterplot which has one variable on the x-axis, one on the y-axis and a point for each case in your dataset. If one variable is explanatory and the other is outcome, it is a very, very strong convention to put the outcome on the y (vertical) axis. One or two additional categorical variables can be accommodated on the scatterplot by encoding the additional information in the symbol type and/or color.
	An example is shown in figure . Age vs. strength is shown, and different colors and symbols are used to code political party and gender.

In a nutshell: You should always perform appropriate EDA before further analysis of your data. Perform whatever steps are necessary to become more familiar with your data, check for obvious mistakes, learn about variable distributions, and learn about relationships be- tween variables. EDA is not an exact science – it is a very important art!