Topic 17 | Linear regression using Sklearn

 

 

AI Free Basic Course | Lecture 17 | Linear regression using Sklearn

 

Regression is the technique of supervised learning. There are two techniques in supervised learning, one is classification and other is regression. In classification we predict category / nominal value. Category or nominal value means something that has label; for example smoker /nonsmoker, cat /dog etc and we have to convert them into numerical value by effort.

In prediction, we use the word positive and negative. For example, if a picture is given to the model and how it will predict whether it is picture of cat or not. Positive value in this would be that it is cat as we want to recognize cat. In medical test, the result is either positive or negative. So positive value is the value in which we are more interested to predict. Remember it does not depend upon  whether covid report is positive nor not, it depends what we have set the algorithm about which we are interested to predict. So covid negative could be our positive class if we have to distribute the shirts to non-positive covid persons.

Regression is other technique of supervised learning.  In regression we always predict a numerical value or score. We place a machine to convert the numeric into 0 or 1. Machine here means not physical machine like drill machine , it is means software. When we convert our values to 0 or 1, it becomes classification.

Now we are going to discuss another form of regression in which we predict score. For example, we have to predict score of babar azam, price of house or marks in the exam. There are many algorithms to predict regression. The first algorithm we are going to use is linear regression. As the name suggests it is related to line. So linear regression means it is related to line with the help of which we will make predictions. In linear regression we use line to predict score.

While doing linear regression we draw a line between two axis. Presently are discussing only two axis and linear regression about three or n number of axis would be discussed later.

 

For predicting dependent variable from independent variable we make use of Linear Regression. Data points shown in the diagram are coordinates of showing corresponding values of x to y.  In 2-D there are two numerical values of each point, one is called x coordinate and other is called y coordinate.

After drawing the points, our next task is to draw a line that is close to these points. How to measure the closeness of these points to the line will be discussed later. Now our goal is to draw a line that is close the data points. The line we draw represents the linear regression modal. So the linear regression modal chooses a line. In this way by selecting any point on x-axis and draw a perpendicular line up to the line, the corresponding value would be the prediction.

Let us explain this with the help of an example. Suppose we are going to predict the size of plot against the value of the plot. Size of plot is mentioned along with x-axis and its corresponding value is mentioned against y-axis. If there is a plot having size of 3-marla and its value is Rs.40, 000/- we will fix a data point against  Rs.40, 000/-. We will pick another plot having plot size of 6-Marla and its value is Rs. 60,000/-. We will also fix a data point against Rs.60, 000/- and so on. In this way we would get many spreading data points some of which will be relevant and others would not be relevant. We will draw multiple lines and will observe which line has more data points. How to draw these multiple lines will be discussed in comings blogs. The lines having more data points around it is our desired linear regression model.

If we have two items, intercept and slope, we can draw any type of line. If we have multiple intercepts and slopes, it means we would have many lines. When we find an intercept and slope that is close to our data point, it would be our desired linear regression model which is used to predict.

Now we are going to introduce another concept of machine learning that is loss. It is very useful concept to train the modal in machine learning. More the distance of line from the data point more the loss would be and vice versa. We will move our search systematically from the line having more loss towards line having less loss.

It is pertinent to mention that loss and error can be used interchangeable. These both represent the same concept. More accurately a given line predicts or represents a data point, less the error or loss would be. Less accurately a given line predicts or represents a data point, more the error or loss would be.

Now question arises, why we take square. Suppose we have four points and we draw a line.

1-One point lies at +10 on the graph.

2- Second point lies at -10 on the graph

3-Third point lies at +40 on graph

4- 4^th point lies at -40 on the graph

What happened in this case? When we add all these figures and the result would be zero. In spite the no data point is close to liner regression modal, we have reduced the error to zero. Looks satisfactory! But it is actually not. Let us see how.

So in order to avoid this all the four points must be in positive value. One way to covert negative to positive is to take the square. So mean squared error means we have squared the all errors and then taken the mean of it. More the Mean Square Error more bad line representation is and less the Mean Square Error is, good line representation is. Mean squared error is the loss function.

The other way to convert the negative to positive is to take the absolute value.

Let us summarize it, we are discussing Linear Regression, in linear regression we want to predict a continuous value. For example we want predict what score a batsman will score in a match, either would it be 00, 20, 50,250 etc. In order to verify the prediction we draw linear regression. The straight line drawn in liner regression have slope, intercept and data points around it. Our purpose is to find the line which have more data points around it. In other words, our purpose is to reach a consensus where every body of the family agrees.

We also discussed about the concept of loss function, which means in case the modal is performing bad we impose penalty. With the passage of time, the value of the error diminishes and reach close to zero. Where there are more data points are around the line it is called  optimal line.  The error value at this stage is called Mean Squared Value which we use to avoid zero calculated value which arises due to addition of same positive and negative values.

Now let us move colab.

Linear Regression using Sklearn

---

0. Hope to Skills - Free AI Course

This note book cover the following concepts

1. Visualization

2. Sea born

TRAINING DATA PRE-PROCESSING

The first step in the machine learning pipeline is to clean and transform the training data into a useable format for analysis and modeling.

As such, data pre-processing addresses:

• Assumptions about data shape
• Incorrect data types
• Outliers or errors
• Missing values
• Categorical variables

Note is being shared with you. Now we confirm that our desired file available in uploads. We are using US housing data. Same data set was given in the assignment number 7. In this assignment it was asked to predict the pricing of the house by determining various factors like number of rooms, area of house, the locality in which it exists or the average house income.

At this stage we are going to skip the routine EDA tasks like data cleaning etc. We are going to perform our preliminary steps like:

Importing the library

Loading the Data Set

Data Shape
After loading the dataset, I examine its shape to get a better sense of the data and the information it contains.

# Data shape	print('train data:',full_data.shape)
	train data: (5000, 7)

 

From the data set given above, longitude, latitude house median age total rooms etc etc has been given. Now we can guess that the address columns from the data set given above has nothing to do with our desired prediction and we have to drop it from the data set.  However as nothing more is important than the location and address of the house, but purpose to drop this column from the data set is to simplify the things.

 Now we generate the heatmap to know about the missing values. We see that there is no missing value in this data set.

Missing Data
A heatmap will help better visualize what features as missing the most information.

# Heatmap sns.heatmap(full_data.isnull(),yticklabels = False, cbar = False,cmap = 'tab20c_r') plt.title('Missing Data: Training Set') plt.show()

 

Now we remove the address column as given below

# Remove Address feature full_data.drop('Address', axis = 1, inplace = True)

The code provided above is about dropping the 'Address' column from the DataFrame 'full_data'. Let me explain each part of the code: 1. full_data: This is the DataFrame from which the column 'Address' is being dropped. 2. .drop('Address', axis=1): The drop() method is used to remove a specified column or row from the DataFrame. In this case, the column being dropped is 'Address'. The axis=1 argument indicates that we are dropping a column (as opposed to a row, where axis=0 would be used). 3. inplace=True: This parameter ensures that the operation is performed directly on the DataFrame 'full_data' itself, and the changes are made in place. If inplace=False (which is the default), the drop operation would return a new DataFrame with the specified column removed, leaving the original DataFrame unchanged. So, after running this code, the 'Address' column will be removed from the 'full_data' DataFrame.

Now we remove the missing data

# Remove rows with missing data full_data.dropna(inplace = True)

The code provided above is about removing rows with missing data (NaN values) from the DataFrame 'full_data'. Let's break down the code: 1. full_data: This is the DataFrame from which the rows with missing data will be removed. 2. .dropna(): The dropna() method is used to remove rows with missing values. By default, it removes any row that contains at least one NaN value. If you want to remove rows with missing values only in specific columns, you can pass the subset parameter to specify those columns. 3. inplace=True: This parameter ensures that the operation is performed directly on the DataFrame 'full_data' itself, and the changes are made in place. If inplace=False, the drop operation would return a new DataFrame with the specified rows removed, leaving the original DataFrame unchanged. After running this code, any rows in the 'full_data' DataFrame that contain at least one NaN value will be removed, and the DataFrame will be modified in place. The DataFrame will now contain only rows with complete data (no NaN values).

# Numeric summary full_data.describe()

The code provided above  full_data.describe(), will generate a numeric summary of the DataFrame 'full_data'. The describe() method provides descriptive statistics for the numeric columns in the DataFrame. Let's break down what this function does: 1. full_data: This is the DataFrame for which the numeric summary will be generated. 2. .describe(): This method computes various descriptive statistics for each numeric column in the DataFrame. The statistics include measures like count, mean, standard deviation, minimum value, 25th percentile (Q1), median (50th percentile or Q2), 75th percentile (Q3), and maximum value. The output will be a new DataFrame containing the numeric summary statistics for each numeric column in 'full_data'. It is a great way to get a quick overview of the central tendency, spread, and distribution of the numerical data in the DataFrame.

 

Now we have data set all values of which are numeric and no value in strings or characters exists which needs to be converted into numeric.

 In these value we need to observe the number of values before decimal. We will count it under each column. We will also count the range of these values.

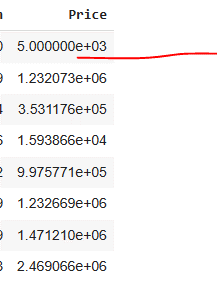
Now look at the value given in the price columns.

The e show the exponential form of price of house. It show how many digit values are available in the value.

Describe gives the five number summary. Look at the count row, it must be same for all columns. If these are not same for all columns than data cleaning needs to be performed in order to make it equal for all columns.

GETTING MODEL READY

Now that we've explored the data, it is time to get these features 'model ready'. Categorical features will need to be converted into 'dummy variables', otherwise a machine learning algorithm will not be able to take in those features as inputs.

Now we see the shape of the data.

# Shape of train data full_data.shape

(5000, 6)

Now the train data is perfect for a machine learning algorithm:

• all the data is numeric
• everything is concatenated together

OBJECTIVE 2: MACHINE LEARNING

Next, I will feed these features into various classification algorithms to determine the best performance using a simple framework: Split, Fit, Predict, Score It.

Target Variable Splitting

We will spilt the Full dataset into Input and target variables. Input is also called Feature Variables Output referes to Target variables.  Our target is to determine the price of the house based on the different features.

As the price column is out target column so we need to make it separate from the data set by removing it.

# Split data to be used in the models # Create matrix of features x = full_data.drop('Price', axis = 1) # grabs everything else but 'Price'

All features have been stored in x as an input except price.

# Create target variable y = full_data['Price'] # y is the column we're trying to predict

 In y as output only price column will exist.

Following will be generated after executing the code.

 

As was told earlier x represents input and y represents output. This convention will be used throughout the course.

Until now we have segregated the values of x-axis and y-axis. Our next step is to take the chunks from this data that would be used for testing and training. For which we use train test function as follows:

# Use x and y variables to split the training data into train and test set from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = .20, random_state = 101)

The code provided above is using the train_test_split function from a machine learning library, likely scikit-learn. This function is used to split a dataset into training and testing sets for building and evaluating machine learning models. Let's break down the code:

1.      x: This is the input feature dataset, typically a DataFrame or a NumPy array, containing the independent variables (features) that will be used to make predictions.

2.      y: This is the target dataset, typically a Series or a NumPy array, containing the dependent variable (target) we are trying to predict.

3.      test_size = .20: This parameter determines the proportion of the data that will be used for testing the model. In this case, 20% of the data will be used for testing, and the remaining 80% will be used for training.

4.      random_state = 101: This parameter is used to set the random seed, ensuring reproducibility of the train-test split. By setting random_state to a fixed value (101 in this case), the data will be split in the same way every time you run the code, making the results consistent.

5.      x_train, x_test, y_train, y_test: These are the variables where the data will be stored after the split. x_train and y_train will contain the training data (input features and target), while x_test and y_test will contain the testing data (input features and target).

After running this code, you will have four datasets: x_train, x_test, y_train, and y_test, which can be used to train and evaluate machine learning models. The model will be trained on x_train and y_train, and then its performance will be evaluated on x_test and y_test.

 

x_train.shape x_train

The first line of code, x_train.shape, will return the shape of the x_train dataset, which is the training set of input features for a machine learning model. It will give you the number of rows and columns in the x_train dataset.

The second line of code, x_train, will display the contents of the x_train dataset itself, which will show you the actual values of the input features used for training the model.

The output of x_train.shape will look something like this (assuming it's a 2-dimensional array)

This means that the x_train dataset has 4000 rows × 5 columns

The output of x_train (if displayed directly) will be the actual content of the x_train dataset, showing the values of the input features. It will be a tabular representation of the data. Since it can be quite large, displaying the entire content might not be practical. The output will depend on the specific data you are working with.

# y_train.shape y_train

The first line of code, y_train.shape, will return the shape of the y_train dataset, which is the training set of target values for a machine learning model. It will give you the number of rows in the y_train dataset.

The second line of code, y_train, will display the contents of the y_train dataset itself, which will show you the actual values of the target variable used for training the model.

The output of y_train.shape will look something like this (assuming it's a 1-dimensional array or a pandas Series):

This means that the y_train dataset has 4000 elements (rows).

The output of y_train (if displayed directly) will be the actual content of the y_train dataset, showing the values of the target variable. It will be a one-dimensional representation of the data. Since it can be quite large, displaying the entire content might not be practical. The output will depend on the specific data you are working with.

In summary, y_train.shape tells you the size of the target variable's training set, and y_train itself shows the actual values of the target variable used for training the machine learning model.

 It means 4000 rows out of 5000 rows have been selected for data training. The columns on the left shows the rows numbers that are selected randomly for data selection.

x_test.shape x_test

The first line of code, x_test.shape, will return the shape of the x_test dataset, which is the testing set of input features for a machine learning model. It will give you the number of rows and columns in the x_test dataset.

The second line of code, x_test, will display the contents of the x_test dataset itself, which will show you the actual values of the input features used for testing the model.

The output of x_test.shape will look something like this (assuming it's a 2-dimensional array):

This means that the x_test dataset has 1000 rows × 5 columns

The output of x_test (if displayed directly) will be the actual content of the x_test dataset, showing the values of the input features. It will be a tabular representation of the data. Since it can be quite large, displaying the entire content might not be practical. The output will depend on the specific data you are working with.

In summary, x_test.shape tells you the size of the input features' testing set, and x_test itself shows the actual values of the input features used for testing the machine learning model.

 

Now the data is in the shape that it can be passed to the modal for training. For which we will import linear regression function from Sklearn library.

 

LINEAR REGRESSION

---

Model Training

# Fit # Import model from sklearn.linear_model import LinearRegression

Explanation:

1.      We import the LinearRegression class from the sklearn.linear_model module.

2.      Next, we create an instance of the LinearRegression model and store it in the variable model.

3.      We use the fit method of the model object to train the linear regression model. The fit method takes two arguments: the training data x_train (input features) and the corresponding target values y_train.

After fitting the model, it learns the coefficients (weights) and the intercept from the training data, and it will be ready to make predictions on new, unseen data.

Keep in mind that fitting a linear regression model assumes a linear relationship between the input features and the target variable. If your data has non-linear relationships, you may need to consider using other regression models or performing feature engineering to capture those patterns effectively.

# Create instance of model lin_reg = LinearRegression()

 Explanation:

1.      You imported the LinearRegression class from the sklearn.linear_model module.

2.      You created an instance of the LinearRegression model and stored it in the variable lin_reg.

Now that you have lin_reg, you can proceed with the model fitting using the fit method, as shown in the previous response. Additionally, you can use lin_reg to access various attributes of the fitted model, such as coefficients and intercept, or use it to make predictions on new data.

LinearRegression LinearRegression()

It seems you want more information about the LinearRegression class and how to use it. Here's a detailed explanation:

Linear Regression: Linear Regression is a simple and widely used statistical technique used for modeling the relationship between a dependent variable (target) and one or more independent variables (features). In a simple linear regression, there is only one independent variable, while in multiple linear regression, there are multiple independent variables.

LinearRegression Class in scikit-learn: LinearRegression is a class provided by scikit-learn (sklearn) library for performing linear regression. It is a part of the sklearn.linear_model module. The LinearRegression class allows you to fit a linear regression model to your data, make predictions using the fitted model, and access the model's attributes such as coefficients and intercept.

Creating an Instance: To use the LinearRegression class, you need to create an instance of it. This is typically done by calling the class with no arguments, as you have done in your code:

Fitting the Model: After creating the instance lin_reg, you can fit the linear regression model to your training data using the fit method. The fit method takes the input features (x_train) and the corresponding target values (y_train) as arguments. It learns the coefficients and the intercept from the training data.

Accessing Model Attributes: Once the model is fitted, you can access its attributes. For example, you can get the coefficients (weights) of the linear regression model using the coef_ attribute and the intercept using the intercept_ attribute.

Making Predictions: After the model is trained, you can use it to make predictions on new, unseen data using the predict method. Pass the input features of the new data as an argument to get the corresponding predicted target values.

Now, y_pred will contain the predicted target values for the x_test data, based on the fitted linear regression model.

Remember, while linear regression is a powerful and widely used technique, it may not be suitable for all types of data or complex relationships. Always evaluate the model's performance and consider other algorithms if needed.

 

# Pass training data into model lin_reg.fit(x_train, y_train)

Here's a brief explanation of the parameters used in the fit method:

·      x_train: This parameter represents the input features or independent variables of your training data. It should be a 2D array-like object (e.g., NumPy array, Pandas DataFrame) with shape (n_samples, n_features), where n_samples is the number of data points (samples) in your training set, and n_features is the number of features (attributes) for each data point.

·      y_train: This parameter represents the target values or dependent variable of your training data. It should be a 1D array-like object (e.g., NumPy array, Pandas Series) with shape (n_samples,), where n_samples is the same as the number of data points in x_train.

The "fit" method is used to train the model on the provided data. After the fitting process, the model will have learned the relationships between the input features and the target values, allowing it to make predictions on new, unseen data.

Keep in mind that different machine learning libraries may use slightly different conventions for fitting models, but the general idea is the same across most libraries. Make sure you have imported the appropriate library (e.g., scikit-learn) and that the lin_reg object is an instance of the linear regression model from that library before calling the fit method.

 

Model Testing

---

Class prediction

# Predict y_pred = lin_reg.predict(x_test) print(y_pred.shape) print(y_pred)

After fitting the linear regression model to the training data, you can use it to make predictions on the test data (x_test). The "predict" method is used for this purpose. It takes the test input features as its parameter and returns the predicted target values.

Here's a brief explanation of the code you provided:

In this code, "y_pred" will be an array-like object containing the predicted target values based on the input features in "x_test." The shape of "y_pred" will be (n_samples,), where n_samples is the number of data points in the test set.

The print statement will display the shape of the predicted values, and then the predicted values themselves will be printed. The actual output will depend on the specific data and model used, but it will be an array of predicted target values for the corresponding data points in "x_test."

 

 

# Combine actual and predicted values side by side results = np.column_stack((y_test, y_pred))

 In the code you provided, you are combining the actual target values from the test set (y_test) with the predicted target values (y_pred) side by side using NumPy's column_stack function. This creates a new NumPy array where the two arrays are stacked as columns.

Here's a brief explanation of the code:

After running this code, the variable results will be a NumPy array with shape (n_samples, 2), where n_samples is the number of data points in the test set. The first column of the results array will contain the actual target values (from y_test), and the second column will contain the corresponding predicted target values (from y_pred).

This combined array can be useful for comparing the actual and predicted values, and you can use it to calculate various metrics to evaluate the performance of your linear regression model on the test data. For example, you can calculate the mean squared error, R-squared score, or other relevant evaluation metrics to assess how well your model is performing on unseen data.

 

Now print the values predicted by the modal and the actual values side by side.

Now from the above values we have taken a value and highlighted it. We see that the difference between the actual value and the predicted value is more.

Difference between the values can be calculated by subtracting the actual value from the predicted value. For this we will find the difference between the actual and predicted value by following method.

# Printing the results print("Actual Values  |  Predicted Values") print("-----------------------------") for actual, predicted in results:     print(f"{actual:14.2f} |  {predicted:12.2f}")

The code you provided is for printing the combined actual and predicted values side by side in a tabular format. This can be useful for visually inspecting the performance of your linear regression model on the test data.

Here's a brief explanation of the code:

The code uses a for loop to iterate over each row of the results array, where each row consists of an actual value and its corresponding predicted value. The f-string formatting is used to align the numbers properly in the table. Each actual value is printed with a field width of 14 characters and two decimal places, while each predicted value is printed with a field width of 12 characters and two decimal places.

The output will look something like this:

This format makes it easy to compare the actual and predicted values for each data point in the test set and visually evaluate how well the model is performing. If the predicted values are close to the actual values, it indicates that the model is making accurate predictions. If there are significant differences between the actual and predicted values, it may suggest that the model needs further improvement.

 Residual Analysis

Residual analysis in linear regression is a way to check how well the model fits the data. It involves looking at the differences (residuals) between the actual data points and the predictions from the model.

In a good model, the residuals should be randomly scattered around zero on a plot. If there are patterns or a fan-like shape, it suggests the model may not be the best fit. Outliers, points far from the others, can also affect the model.

Residual analysis helps ensure the model's accuracy and whether it meets the assumptions of linear regression. If issues are found, adjustments to the model may be needed to improve its performance.

residual = actual- y_pred.reshape(-1) print(residual)

In the code you provided, you are calculating the residuals by subtracting the predicted values (y_pred) from the actual values. To perform this calculation, it seems like you are reshaping the y_pred array to be a 1D array before the subtraction.

Here's a brief explanation of the code:

Explanation:

1.      The line y_pred = results[:, 1] extracts the second column (index 1) from the 'results' array, which contains the predicted values. Since 'results' is a NumPy array with two columns, the first column contains the actual values (y_test) and the second column contains the predicted values (y_pred).

2.      The line y_pred.reshape(-1) reshapes the 'y_pred' array to be a 1D array. The '-1' argument in the reshape method is a placeholder that lets NumPy automatically determine the appropriate size for the reshaped array based on the input shape. In this case, it converts the 'y_pred' array from a 2D shape to a 1D shape.

3.      The line residual = y_test - y_pred.reshape(-1) calculates the residuals by subtracting the predicted values (y_pred) from the actual values (y_test). Since both 'y_test' and 'y_pred' are 1D arrays, the subtraction is element-wise, and it results in a new 1D array called 'residual', which contains the differences between the actual and predicted values for each data point.

The 'residual' array represents the prediction errors for each data point in the test set. Positive values indicate that the model overestimated the target value, while negative values indicate that it underestimated the target value. If the model is accurate, the residuals should be close to zero on average. You can further analyze the residuals to assess the performance of your linear regression model and check for patterns or biases in the predictions.

 

As the difference between the actual and predicted values is great so it show that the modal is not performing good. But the graph as plotted later shows that more data points are around the linear regression line.

As discussed earlier in this lecture the price column of high exponential values which means these are very high value amounts.

The encircled area shows extent of the x-axis and y-axis on the graph. It shows that this graph is 2 x 10 ⁶  alongside x-axis and same is along side y-axis. Which means the difference between the values scaled on x-axis and y-axis are very high so the data points as shown above are not actually very close. As the so big graph cant be drawn so we can say that it is example of optic illusion.

# Distribution plot for Residual (difference between actual and predicted values) sns.distplot(residual, kde=True)

It represents that our mode is not skewed as the distribution is center aligned but note the values of the X and Y axis they in power of 6. Which means the difference between actual and predicted value is very high.

Explanation:

1.      The code imports the required libraries, seaborn for creating the plot and matplotlib.pyplot for adding labels and titles to the plot.

2.      The sns.distplot(residual, kde=True) function is used to create the distribution plot. The residual array, which contains the differences between the actual and predicted values, is passed as the input variable to visualize its distribution. The kde=True argument adds a kernel density estimate to the histogram, providing a smooth line that represents the estimated probability density function of the residuals.

3.      After creating the plot, we add labels to the x-axis and y-axis using plt.xlabel() and plt.ylabel(), respectively.

4.      The plt.title() function is used to set the title of the plot to "Distribution of Residuals."

5.      Finally, plt.show() is called to display the plot.

The resulting plot will show the distribution of the residuals, which can provide insights into the performance of the linear regression model. If the residuals are normally distributed around zero with a symmetric shape, it indicates that the model's predictions are unbiased. However, if the residuals have a skewed or non-symmetric distribution, it suggests that the model might have systematic errors in its predictions. It's essential to examine the distribution plot to understand the behavior of the residuals and identify any potential issues with the model's predictions.

 

 The plot shown above is in the bell shape. The bell curve should be centrally aligned but its height must be lower at the same time. The height shows the difference of predicted value with the actual value.

sns.scatterplot(x=y_test, y=y_pred, color='blue', label='Actual Data points') plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', label='Ideal Line') plt.xlabel('Actual Values') plt.ylabel('Predicted Values') plt.title('Actual (Linear Regression)') plt.legend() plt.show()

 Explanation:

1.      The code imports the required libraries, seaborn and matplotlib.pyplot.

2.      The sns.scatterplot(x=y_test, y=y_pred, color='blue', label='Actual Data points') function creates a scatter plot with the actual values (y_test) on the x-axis and the predicted values (y_pred) on the y-axis. The 'color' parameter is set to 'blue' to use blue color for the data points, and the 'label' parameter is set to 'Actual Data points' to use this label in the legend.

3.      The plt.plot([min(y_test), max(y_test)], [min(y_test), max(y_test)], color='red', label='Ideal Line') function adds a red line to the plot. The line represents the ideal situation where the predicted values perfectly match the actual values. It starts from the point (min(y_test), min(y_test)) and ends at (max(y_test), max(y_test)).

4.      The plt.xlabel('Actual Values') and plt.ylabel('Predicted Values') functions set the labels for the x-axis and y-axis, respectively.

5.      The plt.title('Actual vs. Predicted (Linear Regression)') function sets the title of the plot to 'Actual vs. Predicted (Linear Regression)'.

6.      The plt.legend() function displays the legend on the plot, including the labels 'Actual Data points' and 'Ideal Line'.

7.      Finally, plt.show() is called to display the plot.

The resulting scatter plot will show how well the linear regression model's predictions match the actual values. Data points close to the red ideal line indicate accurate predictions, while points scattered away from the line represent prediction errors. By examining the scatter plot, you can visually assess the performance of your linear regression model and identify any patterns or trends in its predictions.

 

Model Evaluation

# Score It from sklearn.metrics import mean_squared_error   print('Linear Regression Model') # Results print('--'*30) # mean_squared_error(y_test, y_pred) mse = mean_squared_error(y_test, y_pred) rmse = np.sqrt(mse)   # Print evaluation metrics print("Mean Squared Error:", mse) print("Root Mean Squared Error:", rmse)

Now we discuss the loss function that was mentioned in theoretical part above. Mean Square error can be calculated as follows:

Import Mean Square Error from SK learn. 

Take the mean_squared_error function and take both actual values and values predicted by model and placed in mse variable.

mse = mean_squared_error(y_test, y_pred)

When we execute the code above, we get the following output:

Mean Squared Error: 10100187858.864885 Root Mean Squared Error: 100499.69083964829

The Mean squared Error value is very high, but it must be close to zero. That is another proof that the model will not perform good.

As we discussed earlier that we are taking square while calculating Mean Squared Error.

rmse = np.sqrt(mse)

In order to reverse the squre taken already we take square root. The values converted to kilometers by taking square from meters. In order to cancel the affect of square we take square root.

Root Mean Squared Error: 100499.69083964829

The resultant value will give the true picture of error.

Explanation:

1.      The code imports the mean_squared_error function from scikit-learn's sklearn.metrics module.

2.      The line mse = mean_squared_error(y_test, y_pred) calculates the Mean Squared Error (MSE) by comparing the actual values (y_test) with the predicted values (y_pred). The MSE is a common metric used to quantify the average squared difference between predicted and actual values. A lower MSE indicates better model performance.

3.      The line rmse = np.sqrt(mse) calculates the Root Mean Squared Error (RMSE) by taking the square root of the MSE. RMSE is another commonly used metric for regression tasks and represents the square root of the average squared difference between predicted and actual values. Like MSE, a lower RMSE indicates better model performance.

4.      The final two lines of code print the evaluation metrics MSE and RMSE to the console.

After running this code, you will see the MSE and RMSE values for the linear regression model's predictions on the test data. These metrics provide insights into how well the model is performing, with lower values indicating better accuracy. Comparing the MSE and RMSE with other models or benchmarks can help you assess the effectiveness of your linear regression model for the given task.

 Interpretation

Accuracy
MSE is very high Here are some Questions for you

1. what are the possible reasons for higher MSE Values

2. what can we do to lower the value of MSE.